
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< CHAPTER 17. Interpolation | Contents | 17.2 Linear Interpolation >
Interpolation Problem Statement¶
Assume we have a data set consisting of independent data values, \(x_i\), and dependent data values, \(y_i\), where \(i = 1,\ldots, n\). We would like to find an estimation function \(\hat{y}(x)\) such that \(\hat{y}(x_i) = y_i\) for every point in our data set. This means the estimation function goes through our data points. Given a new \(x{\ast}\), we can interpolate its function value using \(\hat{y}(x{\ast})\). In this context, \(\hat{y}(x)\) is called an interpolation function. The following figure shows the interpolation problem statement.
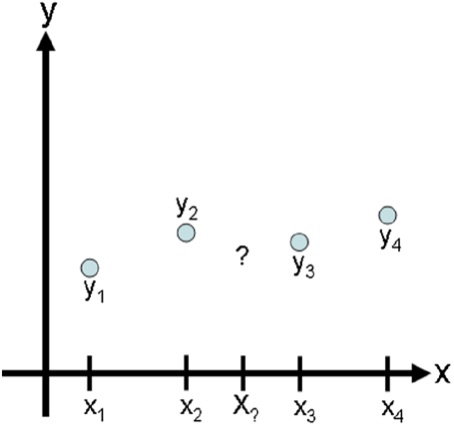
Unlike regression, interpolation does not require the user to have an underlying model for the data, especially when there are many reliable data points. However, the processes that underly the data must still inform the user about the quality of the interpolation. For example, our data may consist of \((x,y)\) coordinates of a car over time. Since motion is restricted to the maneuvering physics of the car, we can expect that the points between the \((x,y)\) coordinates in our set will be “smooth” rather than jagged.
In the following sections we derive several common interpolation methods.
< CHAPTER 17. Interpolation | Contents | 17.2 Linear Interpolation >
