
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< CHAPTER 21. Numerical Integration | Contents | 21.2 Riemann’s Integral >
Numerical Integration Problem Statement¶
Given a function \(f(x)\), we want to approximate the integral of \(f(x)\) over the total interval, \([a,b]\). The following figure illustrates this area. To accomplish this goal, we assume that the interval has been discretized into a numeral grid, \(x\), consisting of \(n+1\) points with spacing, \(h = \frac{b - a}{n}\). Here, we denote each point in \(x\) by \(x_i\), where \(x_0 = a\) and \(x_n = b\). Note: There are \(n+1\) grid points because the count starts at \(x_0\). We also assume we have a function, \(f(x)\), that can be computed for any of the grid points, or that we have been given the function implicitly as \(f(x_i)\). The interval \([x_i, x_{i+1}]\) is referred to as a subinterval.
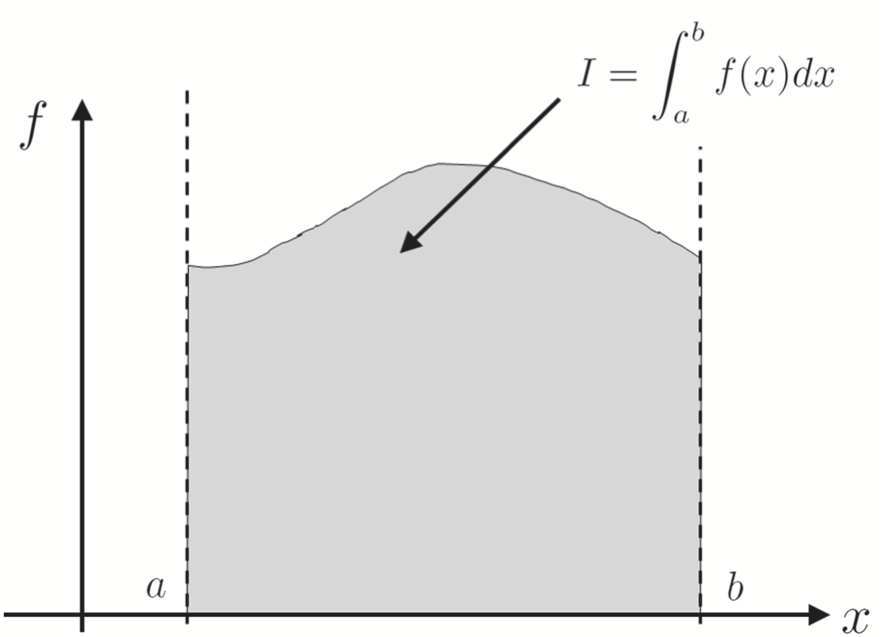
The following sections give some of the most common methods of approximating \(\int_a^b f(x) dx\). Each method approximates the area under \(f(x)\) for each subinterval by a shape for which it is easy to compute the exact area, and then sums the area contributions of every subinterval.
< CHAPTER 21. Numerical Integration | Contents | 21.2 Riemann’s Integral >
