
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< 19.2 Tolerance | Contents | 19.4 Newton-Raphson Method >
Bisection Method¶
The Intermediate Value Theorem says that if \(f(x)\) is a continuous function between \(a\) and \(b\), and \({\text{sign}}(f(a)) \ne {\text{sign}}(f(b))\), then there must be a \(c\), such that \(a < c < b\) and \(f(c) = 0\). This is illustrated in the following figure.
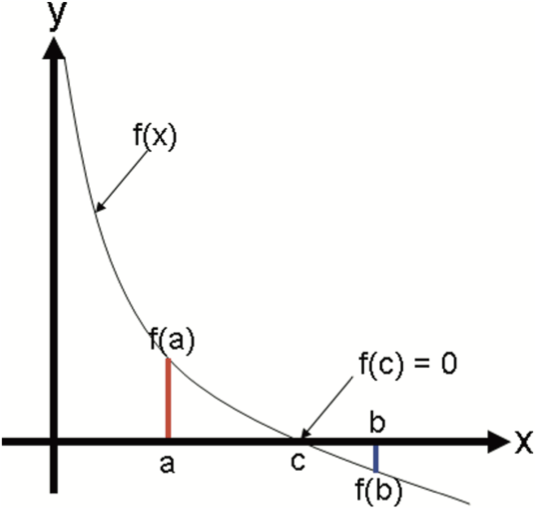
The bisection method uses the intermediate value theorem iteratively to find roots. Let \(f(x)\) be a continuous function, and \(a\) and \(b\) be real scalar values such that \(a < b\). Assume, without loss of generality, that \(f(a) > 0\) and \(f(b) < 0\). Then by the intermediate value theorem, there must be a root on the open interval \((a,b)\). Now let \(m = \frac{b + a}{2}\), the midpoint between and \(a\) and \(b\). If \(f(m) = 0\) or is close enough, then \(m\) is a root. If \(f(m) > 0\), then \(m\) is an improvement on the left bound, \(a\), and there is guaranteed to be a root on the open interval \((m,b)\). If \(f(m) < 0\), then \(m\) is an improvement on the right bound, \(b\), and there is guaranteed to be a root on the open interval \((a,m)\). This scenario is depicted in the following figure.
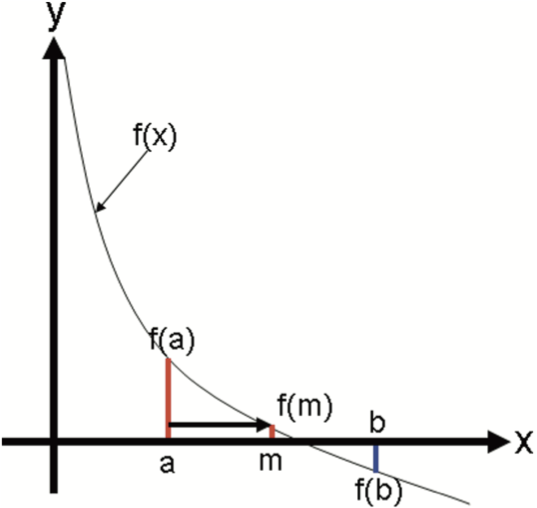
The process of updating \(a\) and \(b\) can be repeated until the error is acceptably low.
TRY IT! Program a function my_bisection(f, a, b, tol) that approximates a root \(r\) of \(f\), bounded by \(a\) and \(b\) to within \(|f(\frac{a + b}{2})| < {\text{tol}}\).
import numpy as np
def my_bisection(f, a, b, tol):
# approximates a root, R, of f bounded
# by a and b to within tolerance
# | f(m) | < tol with m the midpoint
# between a and b Recursive implementation
# check if a and b bound a root
if np.sign(f(a)) == np.sign(f(b)):
raise Exception(
"The scalars a and b do not bound a root")
# get midpoint
m = (a + b)/2
if np.abs(f(m)) < tol:
# stopping condition, report m as root
return m
elif np.sign(f(a)) == np.sign(f(m)):
# case where m is an improvement on a.
# Make recursive call with a = m
return my_bisection(f, m, b, tol)
elif np.sign(f(b)) == np.sign(f(m)):
# case where m is an improvement on b.
# Make recursive call with b = m
return my_bisection(f, a, m, tol)
TRY IT! The \(\sqrt{2}\) can be computed as the root of the function \(f(x) = x^2 - 2\). Starting at \(a = 0\) and \(b = 2\), use my_bisection to approximate the \(\sqrt{2}\) to a tolerance of \(|f(x)| < 0.1\) and \(|f(x)| < 0.01\). Verify that the results are close to a root by plugging the root back into the function.
f = lambda x: x**2 - 2
r1 = my_bisection(f, 0, 2, 0.1)
print("r1 =", r1)
r01 = my_bisection(f, 0, 2, 0.01)
print("r01 =", r01)
print("f(r1) =", f(r1))
print("f(r01) =", f(r01))
r1 = 1.4375
r01 = 1.4140625
f(r1) = 0.06640625
f(r01) = -0.00042724609375
TRY IT! See what will happen if you use \(a = 2\) and \(b = 4\) for the above function.
my_bisection(f, 2, 4, 0.01)
---------------------------------------------------------------------------
Exception Traceback (most recent call last)
<ipython-input-3-4158b7a9ae67> in <module>
----> 1 my_bisection(f, 2, 4, 0.01)
<ipython-input-1-36f06123e87c> in my_bisection(f, a, b, tol)
10 if np.sign(f(a)) == np.sign(f(b)):
11 raise Exception(
---> 12 "The scalars a and b do not bound a root")
13
14 # get midpoint
Exception: The scalars a and b do not bound a root
