
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< 19.4 Newton-Raphson Method | Contents | CHAPTER 20. Numerical Differentiation >
Summary¶
Roots are an important property of functions.
The bisection method is a way of finding roots based on divide and conquer. Although stable, it might converge slowly compared to the Newton-Raphson method.
The Newton-Raphson method is a different way of finding roots based on approximation of the function. The Newton-Raphson method converges quickly close to the actual root, but can have unstable behavior.
Problems¶
Write a function \(my\_nth\_root(x, n, tol)\), where \(x\) and \(tol\) are strictly positive scalars, and \(n\) is an integer strictly greater than 1. The output argument, \(r\), should be an approximation \(r = \sqrt[N]{x}\), the \(N\)-th root of \(x\). This approximation should be computed by using the Newton Raphson method to find the root of the function \(f(y) = y^N - x\). The error metric should be \(|f(y)|\).
Write a function \(my\_fixed\_point(f, g, tol, max_iter)\), where \(f\) and \(g\) are function objects and \(tol\) and \(max\_iter\) are strictly positive scalars. The input argument, \(max\_iter\), is also an integer. The output argument, \(X\), should be a scalar satisfying \(|f(X) - g(X)| < tol\); that is, \(X\) is a point that (almost) satisfies \(f(X) = g(X)\). To find \(X\), you should use the Bisection method with error metric, \(|F(m)| < tol\). The function \(my\_fixed\_point\) should “give up” after \(max\_iter\) number of iterations and return \(X = []\) if this occurs.
Why does the bisection method fail for \(f(x) = 1/x\) with error given by \(|b-a|\)? Hint: How does \(f(x)\) violate the intermediate value theorem?
Write a function \(my\_bisection(f, a, b, tol)\), that returns \([R, E]\), where \(f\) is a function object, \(a\) and \(b\) are scalars such that \(a < b\), and \(tol\) is a strictly positive scalar value. The function should return an array, \(R\), where \(R[i]\) is the estimation of the root of \(f\) defined by \((a + b)/2\) for the \(i\)-th iteration of the bisection method. Remember to include the initial estimate. The function should also return an array, \(E\), where \(E[i]\) is the value of \(| f(R[i]) |\) for the \(i\)-th iteration of the bisection method. The function should terminate when \(E(i) < tol\). You may assume that \({\text{sign}}(f(a)) \neq {\text{sign}}(f(b))\).
Clarification: The input \(a\) and \(b\) constitute the first iteration of bisection, and therefore \(R\) and \(E\) should never be empty.
Test Cases:
In: f = lambda x: x**2 - 2
[R, E] = my_bisection(f, 0, 2, 1e-1)
Out: R = [1, 1.5, 1.25, 1.375, 1.4375]
E = [1, 0.25, 0.4375, 0.109375, 0.06640625]
In: f = lambda x: np.sin(x) - np.cos(x)
[R, E] = my_bisection(f, 0, 2, 1e-2)
Out: R = [1, 0.5, 0.75, 0.875, 0.8125, 0.78125]
E = [0.30116867893975674, 0.39815702328616975, 0.05005010885048666, 0.12654664407270177, 0.038323093040207645, 0.005866372111545948]
Write a function \(my\_newton(f, df, x0, tol)\), that returns \([R, E]\), where \(f\) is a function object, \(df\) is a function object to the derivative of \(f\), \(x0\) is an initial estimation of the root, and \(tol\) is a strictly positive scalar. The function should return an array, \(R\), where \(R[i)]\) is the Newton-Raphson estimation of the root of \(f\) for the \(i\)-th iteration. Remember to include the initial estimate. The function should also return an array, \(E\), where \(E[i]\) is the value of \(| f(R[i]) |\) for the \(i\)-th iteration of the Newton-Raphson method. The function should terminate when \(E(i) < tol\). You may assume that the derivative of \(f\) will not hit 0 during any iteration for any of the test cases given.
Test Cases:
In: f = lambda x: x**2 - 2
df = lambda x: 2*x
[R, E] = my_newton(f, df, 1, 1e-5)
Out: R = [1, 1.5, 1.4166666666666667, 1.4142156862745099]
E = [1, 0.25, 0.006944444444444642, 6.007304882871267e-06]
In: f = lambda x: np.sin(x) - np.cos(x)
df = lambda x: np.cos(x) + np.sin(x)
[R, E] = my_newton(f, df, 1, 1e-5)
Out: R = [1, 0.782041901539138, 0.7853981759997019]
E = [0.30116867893975674, 0.004746462127804163, 1.7822277875723103e-08]
Consider the problem of building a pipeline from an offshore oil platform, a distance \(H\) miles from the shoreline, to an oil refinery station on land, a distance \(L\) miles along the shore. The cost of building the pipe is \(C_{\text{ocean}/\text{mile}}\) while the pipe is under the ocean and \(C_{\text{land}/\text{mile}}\) while the pipe is on land. The pipe will be built in a straight line toward the shore where it will make contact at some point, \(x\), between 0 and \(L\). It will continue along the shore on land until it reaches the oil refinery. See the figure for clarification.
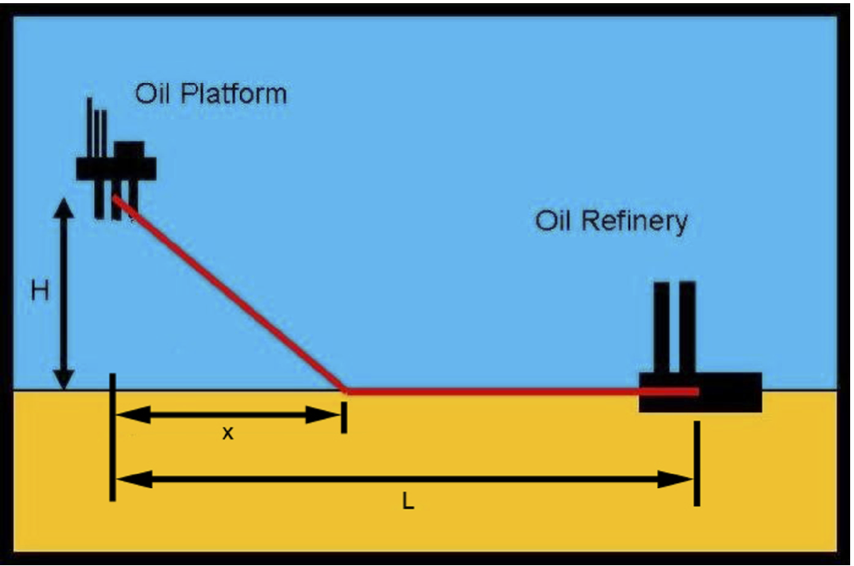
Write a function \(my\_pipe\_builder(C\_ocean, C\_land, L, H)\), where the input arguments are as described earlier, and \(x\) is the x-value that minimizes the total cost of the pipeline. You should use the bisection method to determine this value to within a tolerance of \(1\times10^{-6}\) starting at an initial bound of \(a=0\) and \(b=L\).
Test Cases:
In: my_pipe_builder(20, 10, 100, 50)
Out: 28.867512941360474
In: my_pipe_builder(30, 10, 100, 50)
Out: 17.677670717239380
In: my_pipe_builder(30, 10, 100, 20)
Out: 7.071067392826080
Find a function \(f(x)\) and guess for the root of \(f, x_0\), such that the Newton-Raphson method would oscillate between \(x_0\) and \(-x_0\) indefinitely.
< 19.4 Newton-Raphson Method | Contents | CHAPTER 20. Numerical Differentiation >
